ホーム/ ゲーム/ カジュアルインテリジェンス/ Chromatic puzzle

Chromatic puzzle 1.1.6 MOD APK for Android

Chromatic puzzle
バージョン 1.1.6
更新日 June 25, 2025
カテゴリ カジュアルインテリジェンス
サイズ 23.44MB
7.1
1
2
3
4
5

7.1

ダウンロード(23.44MB)

タイマーなしでパズルゲームをリラックスしてください。目的は、最も少ない色の数を使用することです。

クロマティックそれはタイマーなしのリラックスパズルゲームです。

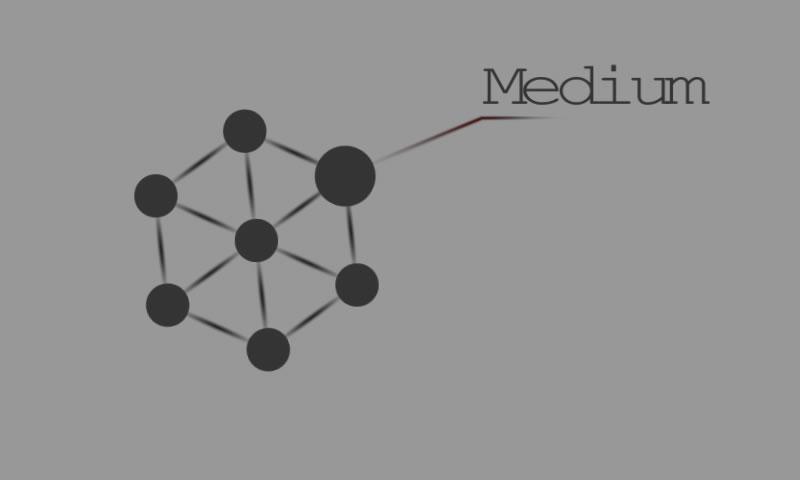
すべての頂点を色付けする必要があります。それだけです！しかし...隣接する頂点は同じ色を持つことはできません。

したがって、目的は最も少ない色の数を使用することであり、グラフの色の数は、色に十分な色の数が少ないことです。

頂点の着色から始めます。ここでは、隣接する頂点が異なる色を取得するようにグラフの頂点を色付けします。簡単な例から始めて、より複雑なグラフに進みます。時々それは簡単です - 時々それは非常に難しいです。

数学の歴史の少し：

グラフの色の数は、グラフの頂点を着色するのに必要な最小数の色であり、2つの隣接する頂点が同じ色を共有しないようにします。

グラフの着色に関する最初の結果は、マップの着色の形で平面グラフをほぼ排他的に扱っています。イングランドの郡の地図を着色しようとしている間、フランシス・ガスリーは4つの色の推測を仮定し、4色がマップを着色するのに十分であるため、共通の境界線を共有する領域が同じ色を受け取らないようにしました。ガスリーの兄弟は、1852年にウィリアム・ハミルトンへの手紙で言及した数学の教師オーガスタス・デ・モーガンに質問を伝えました。アーサー・ケイリーは1879年にロンドン数学協会の会議で問題を提起しました。彼の功績により、ケンペは王立協会のフェローと後にロンドン数学協会の会長に選出されました。

最新バージョン1.1.6の新しいもの

2015年10月12日に最後に更新されたのは、ハードウェアメニュー「バック」とメニュー「メニュー」にサポートを追加しました。
コールするときに一時停止します。
Chromatic puzzle
Chromatic puzzle
Chromatic puzzle
Chromatic puzzle
同様の推奨事項